This looks like a theorem that is going to need a lot of construction lines and diagrams to prove, but I think it can be done with some fairly simple algebra. There is quite a bit of preparation to be done first, but the key is knowing about lines and how to represent them with Plücker coordinates.
A line in space can be conveniently specified by its direction and moment. The direction of the line is given by any vector parallel to the line, \(\vec{\omega}\) say. If \(\vec{p}\) is the position vector of any point on the line then the moment of the line is given by, \[\vec{v}=\vec{p}\times\vec{\omega}.\] Notice that, any other point on the line would be represented by a position vector \(\vec{p}+\lambda\vec{\omega}\) for some constant \(\lambda\), and hence would give the same moment vector since, \[(\vec{p}+\lambda\vec{\omega})\times\vec{\omega}=\vec{p}\times\vec{\omega}.\] There is another way to look at these coordinates for a line, this time we consider lines in the projective space \(\mathbb{P}^3\). A point in this space has homogeneous coordinates \(\tilde{p}=(p_1:\,p_2:\,p_3:\,p_0)\) and the line joining two such points \(\tilde{p}\) and \(\tilde{q}\) has Plücker coordinates, \[P_{ij}=p_iq_j-p_jq_i,\qquad i,\,j=0,\,1,\,2,\,3\] clearly \(P_{ii}=0\) and \(P_{ij}=-P_{ji}\), so there are only 6 independent coordinates. The connection with the direction-moment description becomes clear if we restrict attention to an affine patch of \(\mathbb{P}^3\) by setting \(p_0=q_0=1\) and assuming that \(p_1,\,p_2\) and \(p_3\) are the \(x,\,y\) and \(z\) coordinates respectively of the points. Then we can see that the direction vector of the line is, \[\begin{pmatrix} P_{01}\\ P_{02}\\ P_{03} \end{pmatrix}=\vec{\omega}\quad\text{and}\quad \begin{pmatrix} P_{23}\\P_{31}\\P_{12} \end{pmatrix}=\vec{v}=\vec{p}\times\vec{\omega}\] is the moment of the line. We can write the Plücker coordinates of a line as a 6-vector, \[\ell=\begin{pmatrix} P_{01}\\ P_{02}\\ P_{03}\\P_{23}\\ P_{31}\\ P_{12} \end{pmatrix} =\begin{pmatrix} \vec{\omega}\\ \vec{p}\times\vec{\omega} \end{pmatrix} \] Not all of these 6-component vectors represent lines in 3-dimensions. Given an arbitrary 6-D vector, \[ \mathbf{s}=\begin{pmatrix} Q_{01}\\ Q_{02}\\ Q_{03}\\Q_{23}\\ Q_{31}\\ Q_{12} \end{pmatrix}=\begin{pmatrix} \vec{\omega}\\ \vec{v} \end{pmatrix} \] this represents a line in space if, \[\vec{\omega}\cdot\vec{v}= Q_{01}Q_{23}+Q_{02}Q_{31}+Q_{03}Q_{12}=0.\] This relation can be written as, \[\mathbf{s}^TQ_0\mathbf{s}=0\] where \(Q_0\) is the \(6\times6\) matrix, \[Q_0=\begin{pmatrix} 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1\\ 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&1&0&0&0 \end{pmatrix} = \begin{pmatrix} 0&I_3\\ I_3&0 \end{pmatrix} \] and \(I_3\) is the \(3\times3\) identity matrix.
Now, suppose we have 2 lines in space \(\ell_1\) and \(\ell_2\), and we take the product, \[ \ell_1^TQ_0\ell_2= \begin{pmatrix}\vec{\omega}_1^T&(\vec{p}_1\times\vec{\omega}_1)^T\end{pmatrix} \begin{pmatrix}0&I_3\\I_3&0\end{pmatrix} \begin{pmatrix} \vec{\omega}_2\\\vec{p}_2\times\vec{\omega}_2 \end{pmatrix}= \vec{\omega}_\cdot(\vec{p}_2\times\vec{\omega}_2)+(\vec{p}_1\times\vec{\omega}_1)\cdot\vec{\omega}_2= (\vec{p}_1-\vec{p}_2)\cdot(\vec{\omega}_1\times\vec{\omega}_2). \] Notice that this quantity vanishes if and only if either: the lines are parallel (\(\vec{\omega}_1\times\vec{\omega}_2=0\)), or the lines meet (\(\vec{p}_1=\vec{p}_2\)). This can be summarised as: \(\ell_1^TQ_0\ell_2=0\) if and only if the lines \(\ell_1\) and \(\ell_2\) are co-planar.
The condition for the lines to be perpendicular is then just, \[\ell_1^TQ_{\infty}\ell_2=0\] where, \[Q_{\infty}=\begin{pmatrix} I_3&0\\ 0&0 \end{pmatrix}. \] So lines meet at right-angles if and only if both, \[\ell_1^TQ_{\infty}\ell_2=0\quad\text{and}\quad\ell_1^TQ_0\ell_2=0.\]
The 6-dimensional vectors, all of them not just the lines, have a useful interpretation as the Lie algebra to the Lie group of proper rigid-body displacements in space. This Lie group is usually denoted \(SE(3)\), standing for the special Euclidean group in 3D.
A Lie algebra is a vector space with an anti-symmetric product that satisfies the Jacobi identity. Often the product will be the matrix commutator, which is anti-symmetric and automatically satisfies the Jacobi identity. The commutator of two matrices \(A\) and \(B\) is given by, \[ [A,\,B]=AB-BA\] and it is clear that this is anti-symmetric, \([A,\,B]=-[B,\,A]\). Then computing the triple product of three matrices \(A,\,B\) and \(C\) we have, \[\begin{split} \big[A,\,[B,C]\big]&=ABC-ACB-BCA+CBA,\\ \big[B,\,[C,A]\big]&=BCA-BAC-CAB+ACB,\\ \big[C,\,[A,B]\big]&=CAB-CBA-ABC+BAC. \end{split} \] Summing these three commutators gives the Jacobi identity since all the terms on the right-hand-side will cancel, \[\big[A,\,[B,C]\big]+\big[B,\,[C,A]\big]+\big[C,\,[A,B]\big]=0\]
In our case six dimensional vectors can be represented by \(4\times4\) matrices, \[\mathbf{s}=\begin{pmatrix} Q_{01}\\ Q_{02}\\ Q_{03}\\Q_{23}\\ Q_{31}\\ Q_{12} \end{pmatrix}=\begin{pmatrix} \vec{\omega}\\ \vec{v} \end{pmatrix} \quad\longrightarrow\quad S=\begin{pmatrix} 0&-Q_{03}&Q_{02}&Q_{23}\\ Q_{03}&0&-Q_{01}&Q_{31}\\ -Q_{02}&Q_{01}&0&Q_{12}\\ 0&0&0&0 \end{pmatrix}=\begin{pmatrix} \Omega&\vec{v}\\ 0&0 \end{pmatrix} \] Here, the matrix \(\Omega\) has the property that \(\Omega \vec{u}=\vec{\omega}\times\vec{u}\) for any vector \(\vec{u}\). A straightforward but tedious calculation shows that the commutator of two such matrices corresponds the following product of 6-vectors, \[ [S_1,\,S_2]\quad\longrightarrow\quad\mathbf{s}_1\times\mathbf{s}_2=\begin{pmatrix} \vec{\omega}_1\times\vec{\omega}_2\\ \vec{\omega}_1\times\vec{v}_2+\vec{v}_1\times\vec{\omega}_2 \end{pmatrix}.\] Traditionally, these 6-vectors are called twists and can be used to represent the generalised velocity of a rigid-body. The vector \(\vec{\omega}\) is the instantaneous angular velocity of the body and \(\vec{v}\) is the linear velocity of a point on the body that is instantaneously coincident with the origin of out coordinate system. The commutator operation on the twists is called the vector product of twists, hence the overloading of the \(\times\) operator. A twist can be viewed as a line with a pitch. That is, a general twist can be written as, \[\mathbf{s}=\begin{pmatrix} \vec{\omega}\\ \vec{v} \end{pmatrix} = \begin{pmatrix} \vec{\omega}\\ \vec{p}\times\vec{\omega}+h\vec{\omega} \end{pmatrix} \] where \(h\) is a scalar known as the pitch of the twist. The pitch of an arbitrary twist can be computed as, \[h=\frac{\mathbf{s}^TQ_0\mathbf{s}}{2\,\mathbf{s}^TQ_{\infty}\mathbf{s}}. \] If the pitch of a twist is zero then the twist is a line that is an instantaneous pure rotation about the line. If \(\mathbf{s}^TQ_{\infty}\mathbf{s}=0\) the twist is said to have infinite pitch. Every twist has an axis, that is an associated line. The axis of an arbitrary twist is given by, \[ \ell=\begin{pmatrix} \vec{\omega}\\ \vec{v} \end{pmatrix}-\frac{\mathbf{s}^TQ_0\mathbf{s}}{2\,\mathbf{s}^TQ_{\infty}\mathbf{s}} \begin{pmatrix} \vec{0}\\ \vec{\omega} \end{pmatrix}. \]
Suppose that \(\mathbf{s}_1\) and \(\mathbf{s}_2\) are arbitrary but finite pitch twists. The axes of these twists will be written, as \(\ell_1\) and \(\ell_2\) respectively. That is, \[\mathbf{s}_1=\begin{pmatrix} \vec{\omega}_1\\ \vec{p}_1\times\vec{\omega}_1+h_1\vec{\omega}_1 \end{pmatrix} \quad\text{with axis}\quad \ell_1=\begin{pmatrix} \vec{\omega}_1\\ \vec{p}_1\times\vec{\omega}_1 \end{pmatrix} \] and similar for the other twist. Now the two lines \(\ell_1\) and \(\ell_2\) will meet perpendicularly if and only if the twists satisfy, \[\mathbf{s}_1^TQ_{\infty}\mathbf{s}_2=\mathbf{s}_1^TQ_0\mathbf{s}_2=0.\] To see this, first assume that the twists satisfy the relations above. From \(\mathbf{s}_1^TQ_{\infty}\mathbf{s}_2=0\) we have that \(\vec{\omega}_1\cdot\vec{\omega}_2=0\) and so the lines \(\ell_1\) and \(\ell_2\) are perpendicular. Then \(\mathbf{s}_1^TQ_0\mathbf{s}_2=0\) simplifies to, \[ \mathbf{s}_1^TQ_0\mathbf{s}_2=\vec{\omega}_1\cdot(\vec{p}_2\times\vec{\omega}_2)+\vec{\omega}_2\cdot(\vec{p}_1\times\vec{\omega}_1)+(h_1+h_2)\vec{\omega}_1\cdot\vec{\omega}_2 = \vec{\omega}_1\cdot(\vec{p}_2\times\vec{\omega}_2)+\vec{\omega}_2\cdot(\vec{p}_1\times\vec{\omega}_1)=0 \] and hence \(\ell_1^TQ_0\ell_2=0\), implying that the lines meet. On the other hand, if the lines are perpendicular we have that \(\mathbf{s}_1^TQ_{\infty}\mathbf{s}_2=0\) and then since the lines meet \(\ell_1^TQ_0\ell_2=0\) can be extended by adding a multiple of \(\vec{\omega}_1\cdot\vec{\omega}_2\) to show that \(\mathbf{s}_1^TQ_0\mathbf{s}_2=0\).
Next we look at the two scalar triple products, \[\mathbf{s}_1^TQ_{\infty}(\mathbf{s}_2\times\mathbf{s}_3)=\vec{\omega}_1\cdot(\vec{\omega}_2\times\vec{\omega}_3)\] and \[\mathbf{s}_1^TQ_0(\mathbf{s}_2\times\mathbf{s}_3)= \vec{v}_1\cdot(\vec{\omega}_2\times\vec{\omega}_3)+ \vec{v}_2\cdot(\vec{\omega}_3\times\vec{\omega}_1)+ \vec{v}_3\cdot(\vec{\omega}_1\times\vec{\omega}_2). \] Note that both of these are cyclically symmetric so that we have, \[\mathbf{s}_1^TQ_{\infty}(\mathbf{s}_2\times\mathbf{s}_3)=\mathbf{s}_2^TQ_{\infty}(\mathbf{s}_3\times\mathbf{s}_1)= \mathbf{s}_3^TQ_{\infty}(\mathbf{s}_1\times\mathbf{s}_2)\] and \[\mathbf{s}_1^TQ_0(\mathbf{s}_2\times\mathbf{s}_3)=\mathbf{s}_2^TQ_0(\mathbf{s}_3\times\mathbf{s}_1)= \mathbf{s}_3^TQ_0(\mathbf{s}_1\times\mathbf{s}_2).\]
These last two results allow us to say something about the common perpendicular to lines. Let \(\ell_a\) and \(\ell_b\) be two general lines in space, the common perpendicular to these lines is given by the axis of the twist \(\ell_a\times\ell_b\). To see this, note that the product \(\ell_a\times\ell_a\) is not necessarily a line, it is usually a twist with a finite pitch. However the cyclic property of the triple products and the anti-symmetry of the commutator, imply that, \[\ell_a^TQ_{\infty}(\ell_a\times\ell_b)=0,\qquad \ell_a^TQ_0(\ell_a\times\ell_b)=0\] and also that \[\ell_b^TQ_{\infty}(\ell_a\times\ell_b)=0,\qquad \ell_b^TQ_0(\ell_a\times\ell_b)=0.\] Hence we see that \(\ell_a\) meets and is perpendicular to the axis of \(\ell_a\times\ell_b\) and similarly \(\ell_b\) meets and is perpendicular to the axis of \(\ell_a\times\ell_b\). If we call \(\ell_{ab}\) the common perpendicular to the lines \(\ell_a\) and \(\ell_b\) then \(\ell_{ab}\) is the axis of the twist \(\ell_a\times\ell_b\).
In a similar fashion \(\ell_{a(bc)}\), the common perpendicular to the lines \(\ell_a\) and \(\ell_{bc}\), is the axis of the twist \(\ell_a\times(\ell_b\times\ell_c)\). The line \(\ell_a\) meets and is perpendicular to the axis of \(\ell_a\times(\ell_b\times\ell_c)\) because, \[\ell_a^TQ_{\infty}\big(\ell_a\times(\ell_b\times\ell_c)\big)= \ell_a^TQ_0\big(\ell_a\times(\ell_b\times\ell_c)\big)=0.\] Also \(\ell_{bc}\) meets and is perpendicular to the axis of \(\ell_a\times(\ell_b\times\ell_c)\) since \(\ell_{bc}\) is the axis of the twist \(\ell_b\times\ell_c\) and \[(\ell_b\times\ell_c)^TQ_{\infty}\big(\ell_a\times(\ell_b\times\ell_c)\big)= (\ell_b\times\ell_c)^TQ_0\big(\ell_a\times(\ell_b\times\ell_c)\big)=0\]
We now have all the ingredients to prove the theorem.
Proof (Petersen-Morley Theorem)
Let \(\ell\) be the line that meets and is perpendicular to both \(\ell_{a(bc)}\) and \(\ell_{b(ca)}\). This means that we have the relations,
\[\ell^TQ_{\infty}\big(\ell_a\times(\ell_b\times\ell_c)\big)=\ell^TQ_0\big(\ell_a\times(\ell_b\times\ell_c)\big)=0\]
and
\[\ell^TQ_{\infty}\big(\ell_b\times(\ell_c\times\ell_a)\big)=\ell^TQ_0\big(\ell_b\times(\ell_c\times\ell_a)\big)=0.\]
Now from the Jacobi identity we have,
\[\ell_c\times(\ell_a\times\ell_b)=-\ell_b\times(\ell_c\times\ell_a)-\ell_b\times(\ell_c\times\ell_a).\]
Hence, by the linearity of matrix multiplication we must have,
\[\ell^TQ_{\infty}\big(\ell_c\times(\ell_a\times\ell_b)\big)=\ell^TQ_0\big(\ell_c\times(\ell_a\times\ell_b)\big)=0.\]
So we can conclude that the line \(\ell\) meets and is perpendicular to \(\ell_{c(ab)}\).
This proof seems quite satisfying to me. There is no diagram of the lines only algebra. In fact it is not straightforward to draw a diagram of the lines. In figure 1 such a diagram is shown but I wouldn't claim that it's very clear. The blue lines in the diagram are the original arbitrarily chosen lines, Their common perpendiculars are shown in green. The yellow lines are the common perpendiculars to the original lines and the green lines and the red line is perpendicular to the three yellow lines.
According to Tabachnikov, [6] this theorem is a generalisation to 3 dimensions of the well known theorem that the altitudes of a Euclidean triangle are concurrent. Tabachnikov also notes that Arnold pointed out that the analogous theorem for spherical triangles was simply an application of the Jacobi identity in the Lie algebra to the rotation group, \(so(3)\). The original theorem seems to have been proved using projective geometry [5], [1]. But in 1936 Todd used Study's dual vector formulation of line geometry to prove the theorem again, [4]. Todd's proof is quite similar to the one given here but the connection to the Jacobi identity was not made there.
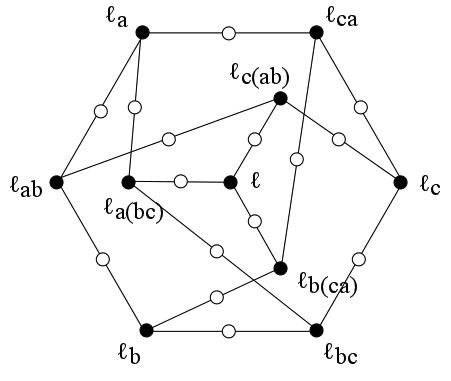
In figure 1 there are 10 lines and 15 points where two lines intersect. There are three points on each line. This is an example of a combinatorial structure known as a configuration or regular uniform design. The incidence relation between the lines and points can be illustrated with a Levi graph, see figure 2. In the figure the filled nodes correspond to lines and the empty nodes to intersection points, edges join lines to the points that lie on them.
Finally a few words about Petersen and Morley. Frank Morley (1860–1937) was born in Woodbridge, Suffolk. After studying Maths at Cambridge he moved the U.S. teaching first at Haverford College in Pennsylvania and then as chair of the Maths dept. at Johns Hopkins University. He supervised some 50 Ph.D. students and published several text books. For over 30 years he was editor of the American Journal of Mathematics. He served as president of the American Mathematical Society in 1919–20. He is probably best known for his theorem on the meets of the trisectors of the angles in an arbitrary triangle, [2]. For a fuller biography of Morley see [4].
Johannes Trolle Petersen (1873–1950) was born in Hørning near Aarhus, Denmark. From 1917 to 1942 he was professor of mathematics at the University of Copenhagen serving as principal for the year 1928–29. He worked in the areas of descriptive geometry and line geometry. In 1904 he changed his name to “Hjelmslev”, the district he was born in. This was to avoid confusion with the graph theorist Julius Peter Christian Petersen. His son Louis Hjelmslev became a well known linguist. This biographical information was taken from [3].
References
[1] H. F. Baker. (1935) “Verification of the Petersen-Morley Theorem”, Proc. London Math. Soc. 11(1):24-26. doi:10.1112/jlms/s1-11.1.24.
[2] A. Bogomolny, “Morley’s Miracle”, Cut The Knot! An interactive column using Java applets, https://www.cut-the-knot.org/triangle/Morley/ Last visit: 28/04/21
[3] Lützen, J. (2020). “The mystery of ten wooden blocks: Hjelmslev’s geometry of reality.” Mathematische Semesterberichte, 67(2):161–167. https://doi.org/10.1007/s00591-020-00275-3 Last visit: 28/04/21
[4] J J O’Connor and E F Robertson, “Frank Morley”, MacTutor History of Mathematics Archive. https://mathshistory.st-andrews.ac.uk/Biographies/Morley/ Last Update October 2003
[5] F. Morley. (1897). “On a regular rectangular configuration of ten lines”. Proc. London Math. Soc., s1-29(1):670–673. https://doi.org/10.1112/plms/s1-29.1.670
[6] S. Tabachnikov. (2016) “Skewers”, Arnold Math. J. 2:171–193. https://doi.org/10.1007/s40598-016-0037-7
[7] J A. Todd. (1936) “Dual Vectors and the Petersen-Morley Theorem”, The Mathematical Gazette ,20(239):184–185. DOI: https://doi.org/10.2307/3608066
[8] Wikipedia,“PetersenMorley theorem”. https://en.wikipedia.org/wiki/Petersen-Morley_theorem Last visit: 28/4/21.